< 문제 출처 >
이공학도를 위한 확률과 통계 3판 한글판

a.
> raw_datas <- read.table("ds13.2.4-vo2max-aerobic-fitness.txt", header=T)
> model_Heart_Rate_at_Rest <- lm(VO2_max ~ Heart_Rate_at_Rest, data = raw_datas)
> plot(model_Heart_Rate_at_Rest, 1)

> model_Body_Fat <- lm(VO2_max ~ Body_Fat, data = raw_datas)
> plot(model_Body_Fat, 1)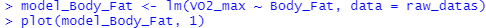

잔차의 등분산성이 잘 유지되는 편으로, 문제 없음을 확인할 수 있습니다.
b.
> model_Weight <- lm(VO2_max ~ Weight, data = raw_datas)
> plot(model_Weight, 1)

몸무게 변수를 모델에 추가할 경우의 그림을 확인해보면 위와 같은 결과를 얻을 수 있고
몸무게 변수가 필요하지 않음을 알 수 있습니다.
c.
> model <- lm(VO2_max ~ Heart_Rate_at_Rest + Body_Fat, data = raw_datas)
> plot(model, 5)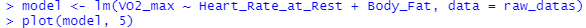

위 그래프에서 확인할 수 있듯이, 회귀모형에 특히 큰 영향을 미치는 데이터가 없습니다.
d.
> model$residuals
1 2 3 4 5 6 7 8 9
-11.5294619 1.0407082 -2.2868629 3.4614630 5.4507601 1.8303309 4.7320449 -1.6883311 2.7311746
10 11 12 13 14 15 16 17 18
6.0132169 -0.9983563 5.0708105 9.1489396 -2.8992000 -6.8197091 -3.8802923 -1.3096306 -3.5586938
19 20
-8.2087337 3.6998232
> library(MASS)
> stdres(model)
1 2 3 4 5 6 7 8 9
-2.1530461 0.1951832 -0.4988211 0.7158809 1.0134656 0.3410078 0.9742454 -0.3168548 0.5190420
10 11 12 13 14 15 16 17 18
1.3359264 -0.1862602 0.9771531 1.9089780 -0.5791683 -1.2967446 -0.7719925 -0.2440824 -0.6705690
19 20
-1.5140557 0.7139798
> plot(raw_datas$VO2_max, stdres(model))

VO2-max가 23일 때의 측정값은 -2.15 standardized residual을 갖습니다.
'About Data > R' 카테고리의 다른 글
| [R Studio][13.4.2][DS13.2.3] 문제풀이 (0) | 2020.12.01 |
|---|---|
| [R Studio][13.2.4][DS13.2.4] 문제풀이 (0) | 2020.12.01 |
| [R Studio][13.3.1][DS13.3.1] 문제 풀이 (0) | 2020.11.30 |
| [R Studio][13.2.3][DS13.2.3] 반응표면모형 (Response Surface) 적합 및 최대값 구하기 예시 (0) | 2020.11.29 |
| [R Studio][13.2.2][DS13.2.2] 반응표면모형 (Response Surface) 적합 및 최대값 구하기 예시 (0) | 2020.11.29 |