< 문제 출처 >
이공학도를 위한 확률과 통계 3판 한글판


a.
> model_depth <- lm(Cost ~ Depth, data = raw_datas)
> plot(model_depth, 1)

> model_downtime <- lm(Cost ~ Downtime, data = raw_datas)
> plot(model_downtime, 1)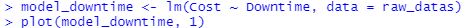
잔차의 등분산성이 잘 유지되는 편으로, 문제 없음을 확인할 수 있습니다.
b.

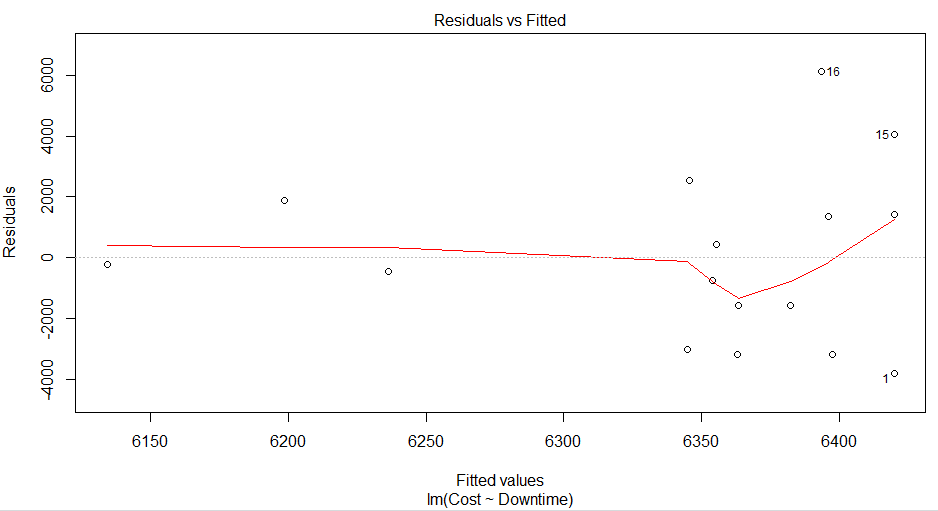
지질학적 특성 변수를 모델에 추가할 경우의 그림을 확인해보면 위와 같은 결과를 얻을 수 있고
지질학적 특성 변수가 필요하지 않음을 알 수 있습니다.
c.
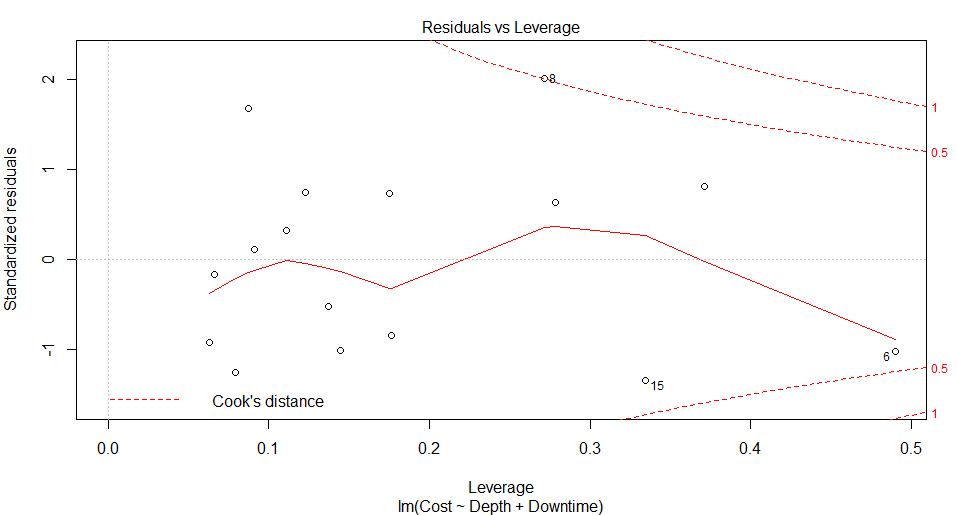
위 그래프에서 확인할 수 있듯이, 점 8과 같은 데이터가 본 회귀모형에 특히 큰 영향을 미친다고 볼 수 있습니다.
즉, 회귀모형에 특히 큰 영향을 미치는 데이터가 있습니다.
d.
> model$residuals
1 2 3 4
410.91948 506.58480 -367.51303 -714.23275
5 6 7 8
81.37131 -561.90253 -584.91748 1311.60597
9 10 11 12
-922.78404 -682.89027 1229.55946 -125.73642
13 14 15 16
535.30644 232.81590 -842.25807 494.07124
> library(MASS)
> stdres(model)
1 2 3 4
0.6328882 0.7297333 -0.5176879 -1.0102345
5 6 7 8
0.1116482 -1.0292303 -0.8432858 2.0104078
9 10 11 12
-1.2582577 -0.9230933 1.6836670 -0.1702421
13 14 15 16
0.7477937 0.3229855 -1.3509677 0.8152291
> plot(raw_datas$Cost, stdres(model))
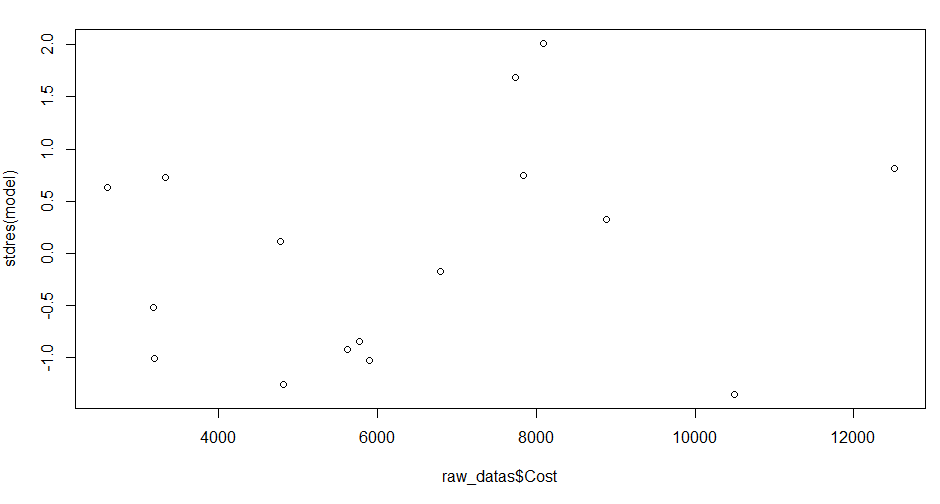
cost가 8095.5일 때의 측정값은 2.01 standardized residual을 갖습니다.
'About Data > R' 카테고리의 다른 글
| [R Studio][13.4.3][DS13.2.4] 문제풀이 (0) | 2020.12.01 |
|---|---|
| [R Studio][13.2.4][DS13.2.4] 문제풀이 (0) | 2020.12.01 |
| [R Studio][13.3.1][DS13.3.1] 문제 풀이 (0) | 2020.11.30 |
| [R Studio][13.2.3][DS13.2.3] 반응표면모형 (Response Surface) 적합 및 최대값 구하기 예시 (0) | 2020.11.29 |
| [R Studio][13.2.2][DS13.2.2] 반응표면모형 (Response Surface) 적합 및 최대값 구하기 예시 (0) | 2020.11.29 |