< 문제 출처 >
이공학도를 위한 확률과 통계 3판 한글판
ds13.2.4-vo2max-aerobic-fitness.txt
0.00MB

1. 데이터 불러오고 심장박동, 체지방률, 몸무게, 나이 모두 포함한 모델로 lm3 생성 및 확인
> raw_datas <- read.table("ds13.2.4-vo2max-aerobic-fitness.txt", header=T)
> raw_datas
VO2_max Heart_Rate_at_Rest Age Body_Fat Weight
1 23 62 59 26 182.0
2 45 59 47 18 175.0
3 29 82 44 22 200.0
4 55 61 32 10 168.5
5 48 60 45 19 193.0
6 42 58 61 22 170.0
7 32 76 71 28 193.0
8 33 70 32 23 218.0
9 34 68 28 27 228.0
10 52 76 36 10 128.0
11 40 67 36 18 167.0
12 35 66 51 29 194.0
13 45 50 31 29 219.0
14 47 57 44 13 215.0
15 26 61 73 28 246.0
16 42 51 47 19 171.0
17 35 60 40 25 212.0
18 41 63 43 16 167.0
19 29 66 68 22 162.0
20 38 57 40 28 239.0
> lm3 <- lm(VO2_max~., data=raw_datas)
> summary(lm3)
Call:
lm(formula = VO2_max ~ ., data = raw_datas)
Residuals:
Min 1Q Median 3Q Max
-10.3426 -3.3262 -0.5895 4.1191 8.2448
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 95.05546 14.64884 6.489 1.02e-05 ***
Heart_Rate_at_Rest -0.36228 0.14997 -2.416 0.0289 *
Age -0.21471 0.09798 -2.191 0.0446 *
Body_Fat -0.77537 0.28823 -2.690 0.0168 *
Weight -0.03530 0.05697 -0.620 0.5449
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 5.167 on 15 degrees of freedom
Multiple R-squared: 0.7197, Adjusted R-squared: 0.645
F-statistic: 9.63 on 4 and 15 DF, p-value: 0.0004602
2. 나이만 포함한 모델 lm3_age 확인
> lm3_age <- lm(VO2_max~Age, data=raw_datas)
> summary(lm3_age)
Call:
lm(formula = VO2_max ~ Age, data = raw_datas)
Residuals:
Min 1Q Median 3Q Max
-11.2953 -4.1037 -0.3734 6.8993 11.5875
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 54.2181 6.1842 8.767 6.49e-08 ***
Age -0.3377 0.1282 -2.634 0.0168 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 7.57 on 18 degrees of freedom
Multiple R-squared: 0.2782, Adjusted R-squared: 0.2381
F-statistic: 6.939 on 1 and 18 DF, p-value: 0.01684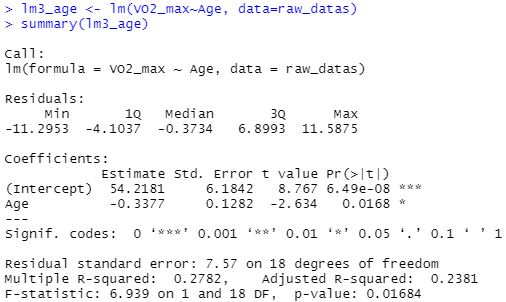
lm3의 residual standard error < lm3_age의 residual standard error
이기때문에 모두 포함된 모델을 선택하는 것이 현명합니다.
3. 최종 모델 도출
lm3의 결과 summary에서 Weight의 경우 p-value가 0.5449로 상당히 크기 때문에 유의하지 않으므로 해당 데이터는 모델에서 제외시킵니다.
> lm3_final <- lm(VO2_max ~ Heart_Rate_at_Rest + Age + Body_Fat, data=raw_datas)
> summary(lm3_final)
Call:
lm(formula = VO2_max ~ Heart_Rate_at_Rest + Age + Body_Fat, data = raw_datas)
Residuals:
Min 1Q Median 3Q Max
-9.645 -3.124 -1.861 4.796 8.296
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 88.82036 10.43735 8.510 2.47e-07 ***
Heart_Rate_at_Rest -0.34282 0.14379 -2.384 0.029841 *
Age -0.19496 0.09084 -2.146 0.047553 *
Body_Fat -0.90070 0.20132 -4.474 0.000384 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 5.067 on 16 degrees of freedom
Multiple R-squared: 0.7126, Adjusted R-squared: 0.6587
F-statistic: 13.22 on 3 and 16 DF, p-value: 0.0001342
- 추정값
βˆ 0 = 88.82036
βˆ 1 = -0.34282
βˆ 2 = -0.19496
βˆ 3 = -0.90070
이므로
Y = 88.82036 - 0.34282 X1 - 0.19496 X2 - 0.90070 X3
입니다.
'About Data > R' 카테고리의 다른 글
| [R Studio][13.4.3][DS13.2.4] 문제풀이 (0) | 2020.12.01 |
|---|---|
| [R Studio][13.4.2][DS13.2.3] 문제풀이 (0) | 2020.12.01 |
| [R Studio][13.3.1][DS13.3.1] 문제 풀이 (0) | 2020.11.30 |
| [R Studio][13.2.3][DS13.2.3] 반응표면모형 (Response Surface) 적합 및 최대값 구하기 예시 (0) | 2020.11.29 |
| [R Studio][13.2.2][DS13.2.2] 반응표면모형 (Response Surface) 적합 및 최대값 구하기 예시 (0) | 2020.11.29 |