< 문제 출처 >
이공학도를 위한 확률과 통계 3판 한글판
ds12.2.5-computer-system-management.txt
/ 0.00MB
[ 문제 ]
DS 12.2.5 의 데이터를 이용하여 표본의 상관계수 r 를 구하고 표본상관계수로 표현되는 t 통계량 t = r√(𝑛 − 2)/√(1 − 𝑟^2)이 t 통계량 t = 𝛽̂ 1/s.e.(𝛽̂ 1)와 같음을 보여라.
> raw_datas <- read.table("ds12.2.5-computer-system-management.txt", header=T)
> cor.test(raw_datas$ActualTime, raw_datas$EstimatedTime)
Pearson's product-moment correlation
data: raw_datas$ActualTime and raw_datas$EstimatedTime
t = 5.7226, df = 30, p-value = 3.034e-06
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
0.4995797 0.8555920
sample estimates:
cor
0.7224266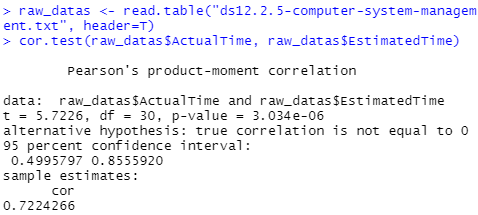
표준 상관 계수 = 0.7224266
t = 5.7226
> lm2 <- lm(ActualTime~EstimatedTime, data=raw_datas)
> summary(lm2)
Call:
lm(formula = ActualTime ~ EstimatedTime, data = raw_datas)
Residuals:
Min 1Q Median 3Q Max
-6.2801 -1.8631 -0.3749 0.8751 8.9582
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -1.9112 1.7598 -1.086 0.286
EstimatedTime 1.6191 0.2829 5.723 3.03e-06 ***
---
Signif. codes:
0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 3.544 on 30 degrees of freedom
Multiple R-squared: 0.5219, Adjusted R-squared: 0.506
F-statistic: 32.75 on 1 and 30 DF, p-value: 3.034e-06
T 통계량 5.723 으로 동일합니다.
'About Data > R' 카테고리의 다른 글
| [R Studio][12.4.7][DS12.2.5] R에서 파일로부터 데이터를 읽고 95% 단측 신뢰구간 구하기 (0) | 2020.11.23 |
|---|---|
| [R Studio][12.9.8][DS12.2.6] 문제 풀이 (0) | 2020.11.23 |
| [R Studio][12.9.3][DS12.2.1] 문제 풀이 (0) | 2020.11.23 |
| [R Studio][12.8.7][DS12.8.5] 문제 풀이 (0) | 2020.11.23 |
| [R Studio][12.8.4][DS12.8.4] 문제 풀이 (0) | 2020.11.23 |